01之间均匀分区取两点构成三角形的概率-证明加代码实现
大约 3 分钟
1. 背景
这是一道我面试字节Data某搜索部门NLP算法工程师岗位出的一道题,可能是由于前面回答问题不是尽如人意,所以一看到这题的时候有点紧张,大概嗯嗯啊啊半分钟,直接心里面觉得自己不会做,便对面试官说想换一个题。等我面试完和同学交流的时候,念完题目就差不多想到了该怎么做,就是个高中的简单整数线性规划问题。
2. 题目描述
假设有一个区间 [0, 1],通过均匀分布取两个点,把区间分成三段,那么这三段构成三角形的概率是多少?
3. 代码解法
既然这是一道编程题,那么其实这个解法就太简单了,根本什么也不用想,直接用代码实现就行了。
import numpy as np
def can_construct_triangle(a, b):
# 使用 任意两边之和大于第三边的性质
a, b = min(a, b), max(a, b)
x = a
y = b - a
z = 1 - b
if x + y > z and x + z > y and y + z > x:
return True
else:
return False
def main():
total_cnt = 0
cnt_be_triangle = 0
for _ in range(1000000):
# 大量随机试验
a = np.random.uniform(0, 1)
b = np.random.uniform(0, 1)
if can_construct_triangle(a, b):
cnt_be_triangle += 1
total_cnt += 1
print(cnt_be_triangle / total_cnt)
# answer is approximate 1/4
if __name__ == "__main__":
main()
用程序跑一下,答案大概是 0.24968,把循环放大一点,就能得到更接近1/4的答案,所以这题的答案应该是1/4。以后遇到不会的数学题,直接用过大量试验求近似解是一个很好的想法。(比如计算机实现牛顿迭代其实就是这么一个思想)
4. 数学解法
4.1 抽丝剥茧看条件
均匀分布取两个点,那么说明两个点是独立同分布,两个点有可能出现在任意位置,任意两个不重合的点可以构成三条边,那么如果要构成三角形,就需要满足构成三角形的条件。
任意两边之和大于第三边 或者是 任意两边之差小于第三边,且每条边大于0。
因此该问题可以转化为不等式求解问题。
4.2 转化为数学表达式
假设随机抽样的两点把 [0, 1] 分成三段,分别是 x, y, 1 - x - y。 因此可以构成一个公式
然后要满足构成三角形的条件,两边之和大于第三边,所以就相当于在上述可行域中找到问题的解空间,这不就是高中非常熟悉的整数线性规划问题吗?只是套了一个均匀分布取两个点的背景。那么看一下三角形两边之和大于第三边的公式是什么?
公式(2)可以进行化简,可以推导出公式(3)
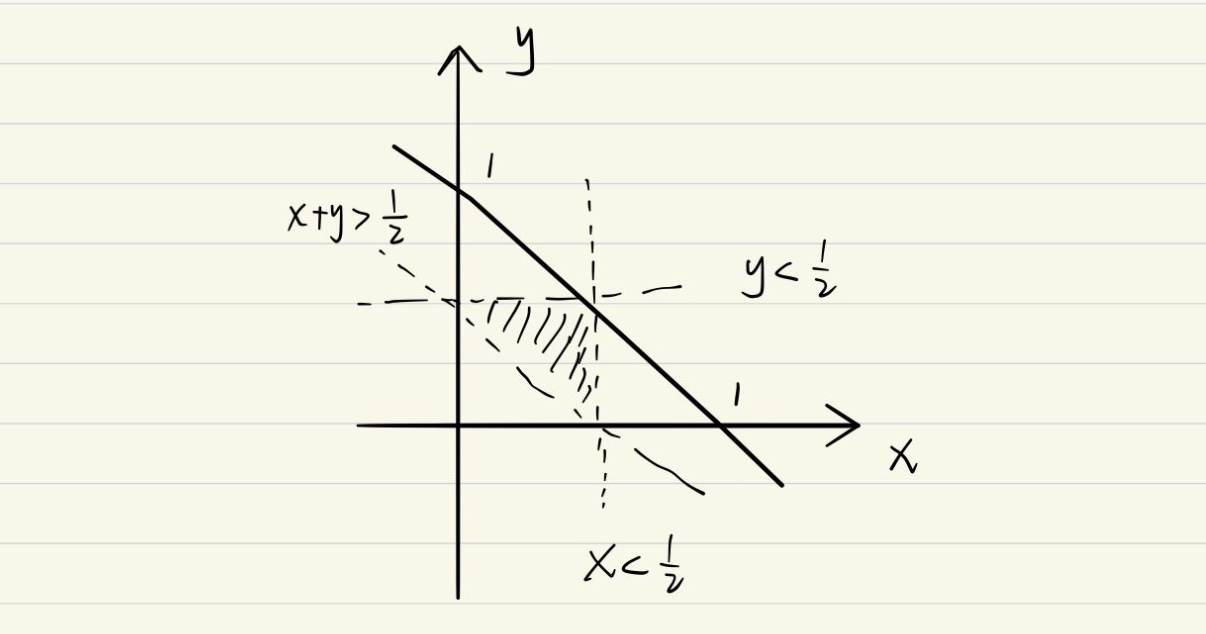
结合公式(1)(3),那么该问题显然是一个简单的数学问题,只要画出图,问题就可以轻易的求解。我的解法配图如下