关于隐马尔可夫模型(HMM)，需要知道什么？

bbruceyuan大约 8 分钟

1. 前言

因为网络上关于隐马尔可夫模型的介绍已经非常多了，而我自认为也写不出比各个博主更优秀的文章，那么因此，在本篇文章中，就以提问的形式解读HMM是什么，可以当作一个HMM只是的速查表。

在阅读本篇文章之前，希望读者已经阅读了李航老师的《统计学习方法》[1]中的第十章，隐马尔科夫模型。

2. HMM是什么？

HMM 是一个序列标注模型，讲的是隐藏的马尔科夫链生成观测序列的过程。通俗的讲就是假定训练数据可以用一条马尔科夫链来描述，然后通过马尔科夫链生成不可观测的隐状态序列(hidden state sequence), 以下用 H 来表示隐状态，再通过隐状态生成观测序列(observation sequence)，以下用 O 表示观测序列。每一个隐状态都能够生成一个观测值，每一个 $i_{i}$ 对应一个 $O_{i}$ 。

对于理解 HMM, HMM的模型结构图必不可少。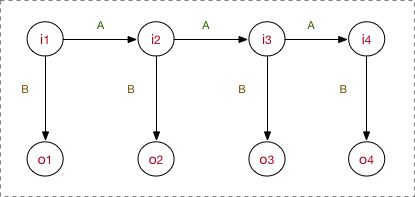
hmm model picture

下一个问题就是解释这个图是什么意思。

3. HMM是用来干什么的？

既然前面提了HMM是一个序列标注模型，那么HMM就可以用来做中文分词、词性标注、实体识别等任务。具体说就是给定一个序列（一句话）：

O = (o_{1}, o_{2}, . . ., o_{t}) w h e r e o_{i} \in {v_{1}, v_{2}, . . ., v_{M}}

这里 V表示所有可能的观测集合,输出另外一个序列：

I = (i_{i}, i_{2}, . . ., i_{t}) w h e r e i_{i} \in {h_{1}, h_{2}, . . ., h_{N}}

这里 $h_{i}$ 可以是 BIO/BMES 之类的标签。

4. HMM的三要素是什么？

状态转移概率矩阵A
观测概率矩阵B
初始状态概率向量 π

π 决定的是初始的状态，π 和 A决定状态序列，确定了隐藏的马尔可夫链，生成不可观测的状态序列；B确定了如何从状态生成观测，与状态序列综合确定了如何产生观测序列。三者可以同意用 $λ = (A, B, π)$ 来表示。

5. HMM的基本假设是什么？

齐次马尔可夫性假设：假设隐藏的马尔可夫链，在任意时刻t的状态，只依赖于其前一时刻的状态，与其它时刻的状态及观测无关，也与时刻t无关。
观测独立性假设: 假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其它观测及状态无关。

以上两个假设其实都是为了简化模型，方便计算之类的。这也是机器学习里面一种很常见的手段。比如语言模型里面的n-gram假设，如果退化成bi-gram就变成了和齐次马尔可夫性假设一致了。而观测独立性假设也很像朴素贝叶斯里面的“在确定类别Y的情况下，特征x之间是条件独立”。

6. HMM的三个问题是什么？

6.1 概率计算有哪几种方法？考虑时间复杂度

已知了 $λ$ 和观测序列 O，计算 $P (O | λ)$ 。有三种非常常见的计算方法，

6.1.1. 直接计算

直接计算的思想很简单，通过穷举所有可能的状态链，假设有t个时间步，一个时间步的状态可能性都是N种，因此所有可能的情况是 N^T种。

重点

问：为什么《统计学习方法》中说直接学习算法的时间复杂度是写的 O(TN^T)，而不是 O(N^T)？回答：上面提到了每一个时间步有 N 中状态情况，一共有T个时间步，所有可能的状态链是N^T。那时间复杂度前面这个T是怎么来的。这里指的是当你算一条可能的状态链的时候，需要经过T个时间步，因此时间复杂度是O(T)，所以总共加起来是O(TN^T)。

这个一个原来比较困扰我的问题，虽然可能大佬一下就看懂了，但是鄙人对于大O表示法理解不深，所以...

6.1.2. 前向算法

前向算法比较好理解，记录下t时刻状态是h_i的情况，因此前向算法中的 $α_{t} (i) = [\sum_{j}^{N} α_{t} (j) a_{j i}] b_{t - 1} (o_{t})$ , 这个公式应该要自己能默写出来才算懂了前向算法。

问：前向算法时间复杂度是什么？答: 因为满足了记忆功能，那么 每次计算的时候，都是两个时间步之间的计算 ，每个时间步可能的状态是N，因此共需要计算N^2, 而一共有T个时间步，所以时间复杂度是 O(TN^2)。时间复杂度从指数级变成了多项式级别。

6.1.3. 后向算法

后向算法和前向算法很像，具体查看李航老师的书。公式如下：

β_{i} (i) = \sum_{j = 1}^{N} π_{i} b_{j} (o_{t + 1}) β_{t + 1} (j)

重点

问：前向算法的 alpha 的初始值很好懂，就是 lambda 中的初始状态参数，那么后向算法种的初始beta值是怎么回事呢，为什么全部初始化为1？答：这里应该先看一下后向算法的定义：在t时候状态为h_i, 并且 t+1 时候的观测值为 $o_{t + 1}, o_{t + 2}, . . ., o_{T}$ 。那么初始值就是在第T个时间步了，T+1时间步已经没有观测值了，所以把他初始化为1。可能有读者会问，为啥因为后面没有T+1了就是初始化为1，可以这么理解，到了最后一个时间步，你必然会到达T时刻的某个隐藏状态，后面不管是啥都可以了，所以认为是1。（好像也没有解释清楚，可以品一品？// 或者讨论一下

同理，后向也有记忆功能，所以时间复杂度是O(TN^2).

总结：前向和后向可以看作是动态规划问题

6.2 通过什么方法学习参数？

已知了观测序列 O，估计可能的 $λ = (A, B, π)$ ，使得 $P (O | λ)$ 最大，变成了参数学习问题。

6.2.1 极大似然估计法

这种方法需要标注很多样本，不使用与大多数情况。极大似然是拟合当前样本分布，所以可以直接计算。（注：这里又很像朴素贝叶斯了

6.2.2. Baum-Welch算法

这显然是一个EM算法(具有隐变量)问题，这里的隐变量就是隐状态I。需要注意的点是如果写出该问题的Q函数。建议配合李航老师的书以及壮哉我贾诩文和open in new window[^2]写的HMM的numpy实现一起参考。

6.3 通过什么方式对序列进行解码？

这也就是预测问题，已知 $λ$ 和O，求最有可能的隐状态 I。因为已知了lambda, 那么可以计算出所有可能的路径，然后选择其中最大的一条，但是这样显然时间复杂度太高了，不够高效，因此可以使用维特比算法完成这个选择。（维特比算法可以用于其他的路径选择问题。维特比算法：只记录过某一个节点的最优路径。这个务必要知道。

7. HMM，MEMM，CRF的区别是什么？

最后这个问题是最有意义的一个问题。

HMM 是一个生成式模型，而MEMM和CRF是判别式模型。

MEMM解决了CRF的观测独立性假设。通过引入自定义的特征函数，可以通过 特征函数 定义观测状态之间的依赖，以及当前观测状态与前后隐藏状态之间的关系。

CRF相对于 MEMM，则是通过全局归一化来解决MEMM的标注偏置的问题。具体的公式体现在：MEMM的累乘符号在归一化外面，所以MEMM是局部归一化，而CRF的累乘符号在归一化内部，所以CRF是全局归一化。

MEMM公式：

P (I | O) = \prod_{t = 1}^{n} \frac{e x p (\sum_{a} λ_{a} f_{a} (O, I_{i})}{Z (O, I_{i - 1})}, i = 1, . . ., n

MEMM是使用的局部归一化，意思就是每做一次状态转移之前，都要进行一次 Softmax，因此倾向于选择转移路径比较少的状态。

CRF公式：

P (I | O) = \frac{\prod_{t = 1}^{n} e x p (\sum_{a} λ_{a} f_{a} (O, I_{i - 1}, I_{i}, i)}{Z (O)}, i = 1, . . ., n

随便抄了两个公式，可能和你在其他地方看到的公式写的不一样。这都是可以自己定义的，不过不要纠结上述两个式子里面的 $f_{a}$ 不相同，因为** $f_{a}$ 可以写成一样的[^4]，不对，应该说两者就应该是一样的** ，但为了和大部分教程写成一样，保留了现在的形式。另一个重点是局部归一化和全局归一化的区别，也就是配分函数Z的位置。

以上整体内容有参考，主要是图片以及整体理解[^3].

8. Reference

[1]. 《统计学习方法》，李航
[2]. https://zhuanlan.zhihu.com/p/75406198
[3]. https://zhuanlan.zhihu.com/p/33397147
[4]. http://www.cs.columbia.edu/~mcollins/crf.pdf

关于隐马尔可夫模型(HMM)，需要知道什么？

# 1. 前言

# 2. HMM是什么？

# 3. HMM是用来干什么的？

# 4. HMM的三要素是什么？

# 5. HMM的基本假设是什么？

# 6. HMM的三个问题是什么？

# 6.1 概率计算有哪几种方法？考虑时间复杂度

# 6.1.1. 直接计算

# 6.1.2. 前向算法

# 6.1.3. 后向算法

# 6.2 通过什么方法学习参数？

# 6.2.1 极大似然估计法

# 6.2.2. Baum-Welch算法

# 6.3 通过什么方式对序列进行解码？

# 7. HMM，MEMM，CRF的区别是什么？

# 8. Reference